lunes, 4 de junio de 2012

limite


  • el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
    El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.


    Propiedades generales
    Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguiente propiedades:

    Límite deExpresión
    Una constante 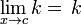\lim_{x \to c} k =\, k\,
    La función identidad 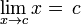\lim_{x \to c} x = \, c \,
    El producto de una función y una constante 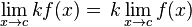\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,
    Una suma 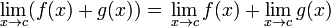\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,
    Una resta \lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,
    Un producto 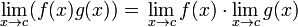\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,
    Un cociente 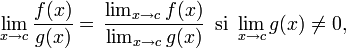\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,
    Una potencia {\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0
    Un logaritmo {\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}
    El número e {\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e
    Función f(x) acotada y g(x) infinitesimal {\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0.


    Indeterminaciones


    OperaciónIndeterminación
    Sustracción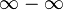\infty - \infty
    Multiplicación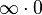\infty \cdot 0
    División\cfrac{\infty}{\infty}, \cfrac{0}{0}
    Elevación a potencia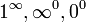1^\infty, \infty ^0, 0^0



    Ejemplo.

    0/0 es una indeterminación, es decir, no es posible, a priori, saber cual es el valor de un límite que tiende a cero sobre otro que también tiende a cero ya que el resultado no es siempre el mismo. Por ejemplo:


Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)